1. There are two types of loops in Python: while and for:
-
- the
whileloop executes a statement or a set of statements as long as a specified boolean condition is true, e.g.:
- the
|
1 2 3 4 5 6 7 8 9 10 |
# Example 1 while True: print("Stuck in an infinite loop.") # Example 2 counter = 5 while counter > 2: print(counter) counter -= 1 |
-
- the
forloop executes a set of statements many times; it’s used to iterate over a sequence (e.g., a list, a dictionary, a tuple, or a set – you will learn about them soon) or other objects that are iterable (e.g., strings). You can use theforloop to iterate over a sequence of numbers using the built-inrangefunction. Look at the examples below:
- the
|
1 2 3 4 5 6 7 8 9 10 |
# Example 1 word = "Python" for letter in word: print(letter, end="*") # Example 2 for i in range(1, 10): if i % 2 == 0: print(i) |
2. You can use the break and continue statements to change the flow of a loop:
-
- You use
breakto exit a loop, e.g.:
- You use
|
1 2 3 4 5 |
text = "Coding in Python" for letter in text: if letter == "P": break print(letter, end="") |
-
- You use
continueto skip the current iteration, and continue with the next iteration, e.g.:
- You use
|
1 2 3 4 5 |
text = "pyxpyxpyx" for letter in text: if letter == "x": continue print(letter, end="") |
3. The while and for loops can also have an else clause in Python. The else clause executes after the loop finishes its execution as long as it has not been terminated by break, e.g.:
|
1 2 3 4 5 6 |
n = 0 while n != 3: print(n) n += 1 else: print(n, "else") |
0
1
2
3 else
|
1 2 3 4 |
for i in range(0, 3): print(i) else: print(i, "else") |
0
1
2
2 else
|
1 2 3 4 5 6 7 8 9 10 11 |
for i in range(5): print(i) else: print("else:", i) 0 1 2 3 4 else: 4 |
The
i variable retains its last value.
|
1 2 3 4 5 6 7 |
i = 111 for i in range(2, 1): print(i) else: print("else:", i) else: 111 |
The loop’s body won’t be executed here at all. Note: we’ve assigned the i variable before the loop. When the loop’s body isn’t executed, the control variable retains the value it had before the loop.
Note: if the control variable doesn’t exist before the loop starts, it won’t exist when the execution reaches the else branch.
4. The range() function generates a sequence of numbers. It accepts integers and returns range objects. The syntax of range() looks as follows: range(start, stop, step), where:
startis an optional parameter specifying the starting number of the sequence (0 by default)stopis an optional parameter specifying the end of the sequence generated (it is not included),- and
stepis an optional parameter specifying the difference between the numbers in the sequence (1 by default.)
Example code:
|
1 2 3 4 5 |
for i in range(3): print(i, end=" ") # Outputs: 0 1 2 for i in range(6, 1, -2): print(i, end=" ") # Outputs: 6, 4, 2 |
Scenario 1
In 1937, a German mathematician named Lothar Collatz formulated an intriguing hypothesis (it still remains unproven) which can be described in the following way:
take any non-negative and non-zero integer number and name it c0;
if it’s even, evaluate a new c0 as c0 ÷ 2;
otherwise, if it’s odd, evaluate a new c0 as 3 × c0 + 1;
if c0 ≠ 1, skip to point 2.
The hypothesis says that regardless of the initial value of c0, it will always go to 1.
Of course, it’s an extremely complex task to use a computer in order to prove the hypothesis for any natural number (it may even require artificial intelligence), but you can use Python to check some individual numbers. Maybe you’ll even find the one which would disprove the hypothesis.
Write a program which reads one natural number and executes the above steps as long as c0 remains different from 1. We also want you to count the steps needed to achieve the goal. Your code should output all the intermediate values of c0, too.
Hint: the most important part of the problem is how to transform Collatz’s idea into a while loop – this is the key to success.
Test your code using the data we’ve provided.
Test Data
Sample input: 15
Expected output:
46
23
70
35
106
53
160
80
40
20
10
5
16
8
4
2
1
steps = 17
Sample input: 16
Expected output:
8
4
2
1
steps = 4
Sample input: 1023
Expected output:
3070
1535
4606
2303
6910
3455
10366
5183
15550
7775
23326
11663
34990
17495
52486
26243
78730
39365
118096
59048
29524
14762
7381
22144
11072
5536
2768
1384
692
346
173
520
260
130
65
196
98
49
148
74
37
112
56
28
14
7
22
11
34
17
52
26
13
40
20
10
5
16
8
4
2
1
steps = 62
Scenario 2
Listen to this story: a boy and his father, a computer programmer, are playing with wooden blocks. They are building a pyramid.
Their pyramid is a bit weird, as it is actually a pyramid-shaped wall – it’s flat. The pyramid is stacked according to one simple principle: each lower layer contains one block more than the layer above.
The figure illustrates the rule used by the builders:
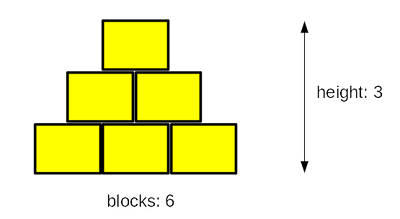
Your task is to write a program which reads the number of blocks the builders have, and outputs the height of the pyramid that can be built using these blocks.
Note: the height is measured by the number of fully completed layers – if the builders don’t have a sufficient number of blocks and cannot complete the next layer, they finish their work immediately.
Test your code using the data we’ve provided.
Test Data
Sample input: 6
Expected output: The height of the pyramid: 3
Sample input: 20
Expected output: The height of the pyramid: 5
Sample input: 1000
Expected output: The height of the pyramid: 44
Sample input: 2
Expected output: The height of the pyramid: 1
Exercise 3
Create a program with a for loop and a break statement. The program should iterate over characters in an email address, exit the loop when it reaches the @ symbol, and print the part before @ on one line. Use the skeleton below:
Solutions 1
|
1 2 3 4 5 6 7 8 9 10 11 |
c0=int(input("c0= ")) i=0 while c0 != 1: if c0%2==0: c0/=2 else: c0=3*c0 + 1 c0=int(c0) print(c0) i+=1 print("steps = ", i) |
Solution 2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
blocks = int(input("Enter the number of blocks: ")) height=0 i=0 while blocks>0: height+=1 blocks-=height print (height, blocks) if height+1 > blocks: break print("The height of the pyramid:", height) |
Solution 3
|
1 2 3 4 |
for ch in "john.smith@pythoninstitute.org": if ch == "@": break print(ch, end="") |
Exercise 5
What is the output of the following code?
|
1 2 3 4 5 6 7 |
n = 3 while n > 0: print(n + 1) n -= 1 else: print(n) |
4
3
2
0
Exercise 6
What is the output of the following code?
|
1 2 3 4 5 6 |
n = range(4) for num in n: print(num - 1) else: print(num) |
-1
0
1
2
3
Exercise 7
What is the output of the following code?
|
1 2 |
for i in range(0, 6, 3): print(i) |
0
3
Ex. 8
Which of the following Python keywords is used as an empty statement that does nothing?
Which of the following statements about the arguments of a function are true?(Select two answers)
Ex. 10
What is the output of the following code snippet?
|
1 2 3 4 5 6 7 |
str = "Monty" for i in str: print(i) break else: print("Python") |
M
Ex. 11
What is the output of the following code snippet?
|
1 2 3 4 5 6 7 8 9 |
str = "XyZ" c = "x" while c not in str: print("A") break else: print("B") |
AB
B
A
The code has no output
What is the output of the following code snippet?
|
1 2 3 4 |
for ch in "Python": pass print(ch) |


